
A veces, el debate entre la media y la mediana puede resultar bastante interesante. Especialmente cuando se observa la inclinación y simetría de los datos estadísticos en un histograma.
Histograma sesgado a la derecha
La representación de tendencias, variables o cualquier cambio en la medición de elementos de cualquier tipo suelen mostrarse en gráficas, es la manera más fácil de mostrar en imagen una tendencia, explicar la proyección negativa o positiva alrededor de un fenómeno o los cambios en el mismo. Dentro de las gráficas de este tipo, los histogramas están entre los más usados ya que permiten mirar con mucha claridad estos cambios, con datos numéricos y una visión que deja ver claramente las diferencias en avances o retrocesos.
Cuando hablamos de un histograma sesgado, estamos refiriéndonos a que hay una tendencia, una inclinación del gráfico a favor o en contra de algo, un crecimiento o decrecimiento, en resumen, que los datos indican que la situación está mejorando o empeorando. En el caso de un histograma sesgado a la derecha, lo interpretamos como un histograma sesgado positivamente.
Simetría de un histograma
Un histograma representa siempre un conjunto de datos, los cambios en estos datos solo los veremos reflejados en el tamaño de las columnas o barras verticales en el histograma.
La forma exacta que tienen estas barras en la gráfica es la de rectángulos. Por asuntos de pulcritud estadística y el reflejo de la misma visualmente, el ancho de los rectángulos debe ser exactamente el mismo. Recordemos que las gráficas reflejan fielmente datos, si en una gráfica de torta (redonda), por un error humano hacemos un fragmento más ancho que otro cuando la realidad es al revés, estamos alterando toda una realidad.
Pero en un histograma la asimetría estará presente porque si utilizamos este gráfico es porque necesitamos plasmar una realidad que se ha alterado, ha cambiado o puede cambiar (proyección) en algún momento en el tiempo.
Histograma asimétrico a la derecha

Siendo la asimetría esa tendencia de cambiar un comportamiento fijo que habíamos notado previamente en una serie de elementos, cuando hablamos de un histograma asimétrico a la derecha, es porque es una asimetría positiva o el histograma esta sesgado positivamente.
Hay que aclarar que, cuando hablamos de realidad de los datos mostrados de manera gráfica, no necesariamente hablamos sobre realidades ya cumplidas o hechos, siendo las gráficas un reflejo de datos pero también de estadísticas de proyección de los mismos, pueden señalar tendencias y probabilidades, como una señal efectiva que permita prepararse para dichos cambios, aprovecharlos o revertirlos con tiempo según sea el caso.
Gráficos de asimetría
Los gráficos de asimetría tienen muchos usos en la vida diaria, todos los hemos visto aunque no los reconozcamos por utilizarlos con poca frecuencia.
Sin importar el país en el que vives, seguramente has visto alguna publicidad o información sobre campañas electorales, sobre datos de infectados o muertos por el COVID-19, para todos estos casos se suelen usar gráficos. A efectos publicitarios lo más común es mirar los histogramas en campañas presidenciales, donde al mirar las barras sobre la gráfica, que deben tener el mismo ancho, notaremos la diferencia de altura, siendo el candidato que “va punteando las encuestas” el que está representado por la barra o rectángulo más alto. Eso es un histograma y se supone que esos datos que hacen las barras más altas o bajas reflejan la asimetría de la realidad dada por los datos.
El promedio
Por ejemplo, suponga que usted es parte de un equipo de la NBA que está tratando de negociar los salarios. Si representas a los propietarios, quieres mostrar cuánto ganan todos y cuánto dinero gastas, así que tienes que tener en cuenta a esos jugadores superestrella y reportar el promedio. Pero si estás del lado de los jugadores, deberías reportar el promedio, porque eso es más representativo de lo que los jugadores del medio están haciendo. El cincuenta por ciento de los jugadores ganan un salario por encima de la mediana, y el cincuenta por ciento ganan un salario por debajo de la mediana.
Media como la mediana
Para resolverlo todo, es mejor encontrar y comparar tanto la media como la mediana. Un gráfico que muestra la forma de los datos es un buen punto de partida.
Uno de los gráficos que puede hacer para ilustrar la forma de los datos numéricos (cuántos valores están cerca o lejos de la media, dónde está el centro, cuántos valores atípicos podría haber) es un histograma. Un histograma es un gráfico que organiza y muestra datos numéricos en forma de imagen, mostrando grupos de datos y el número o porcentaje de los datos que corresponden a cada grupo. Le da una buena instantánea del conjunto de datos.
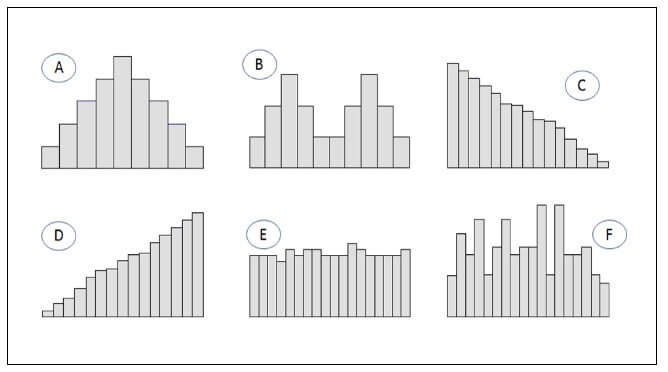
A) Datos sesgados a la derecha; B) datos sesgados a la izquierda; y C) datos simétricos.
Los conjuntos de datos pueden tener muchas formas posibles; aquí hay una muestra de tres formas que se discuten comúnmente en los cursos introductorios de estadística:
- Si la mayoría de los datos se encuentran en el lado izquierdo del histograma, pero algunos valores más grandes se encuentran a la derecha, se dice que los datos están sesgados a la derecha.el histograma A de la figura muestra un ejemplo de datos que están sesgados a la derecha. Los pocos valores más grandes traen la media hacia arriba pero no afectan realmente a la mediana. Por lo tanto, cuando los datos están sesgados a la derecha, la media es mayor que la mediana. Un ejemplo de estos datos serían los salarios de los equipos de la NBA, donde los jugadores estrella ganan mucho más que sus compañeros de equipo.
- Si la mayoría de los datos están a la derecha, con unos pocos valores más pequeños que aparecen en el lado izquierdo del histograma, los datos están sesgados a la izquierda.el histograma B de la figura muestra un ejemplo de datos que están sesgados a la izquierda. Los pocos valores más pequeños reducen la media, y de nuevo la mediana se ve mínimamente afectada (si es que se ve afectada). Un ejemplo de datos sesgados hacia la izquierda es la cantidad de tiempo que los estudiantes usan para tomar un examen; algunos estudiantes se van temprano, otros se quedan más tarde, y muchos se quedan hasta el amargo final (¡algunos se quedarían para siempre si pudieran!). Cuando los datos están sesgados a la izquierda, la media es menor que la mediana.
- Si los datos son simétricos, tienen aproximadamente la misma forma a ambos lados del centro. En otras palabras, si dobla el histograma por la mitad, se ve más o menos igual en ambos lados; el histograma C de la figura muestra un ejemplo de datos simétricos. Con los datos simétricos, la media y la mediana están muy cerca.
Mirando el Histograma A de la figura (cuya forma está sesgada a la derecha), se puede ver que la «cola» del gráfico (donde las barras se están acortando) está a la derecha, mientras que la «cola» está a la izquierda en el Histograma B (cuya forma está sesgada a la izquierda). Al mirar la dirección de la cola de una distribución sesgada, usted determina la dirección de la asimetría. Siempre agregue la dirección cuando describa una distribución sesgada.
El histograma C es simétrico (tiene aproximadamente la misma forma en cada lado). Sin embargo, no todos los datos simétricos tienen una forma de campana como la del Histograma C. Mientras la forma sea aproximadamente la misma en ambos lados, entonces se dice que la forma es simétrica.







